Innehållsöversikt
Kapa brädor och lister
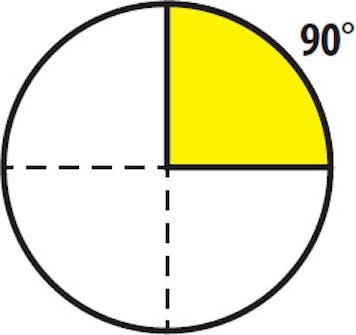
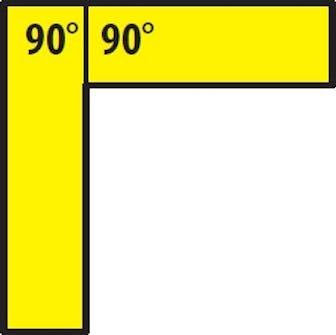
90 grader är det som vi också kallar en rät vinkel. Den är så vanlig att vi sällan tänker på den som 90 grader.
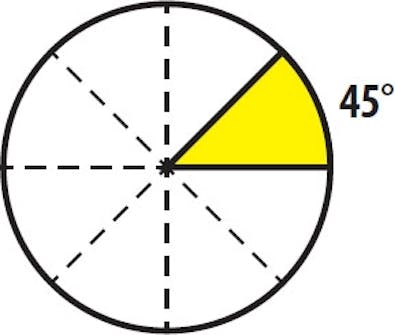
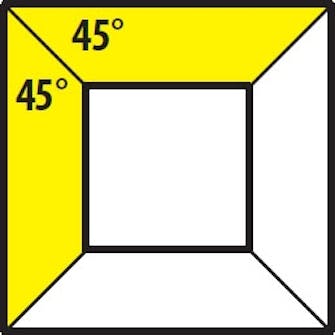
45 grader är den allra vanligaste vinkeln när vi talar om geringssågning. Två bitar sågade i 45 grader bildar en rät vinkel.
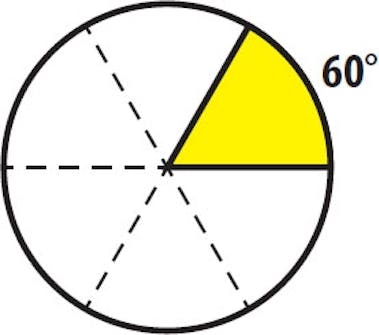
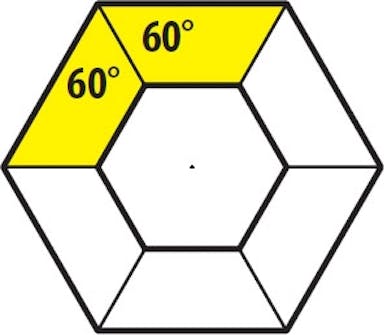
60 grader finner vi i de tre hörnen i en triangel med lika långa sidor. När en cirkel delas i 6 tårtbitar blir varje bit 60 grader.
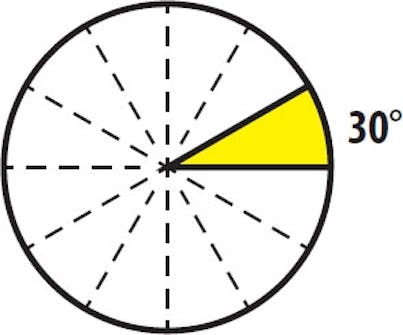
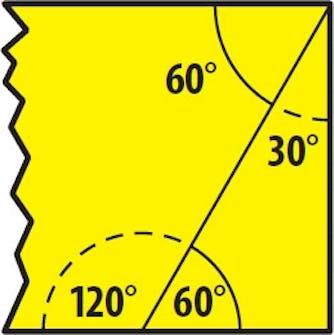
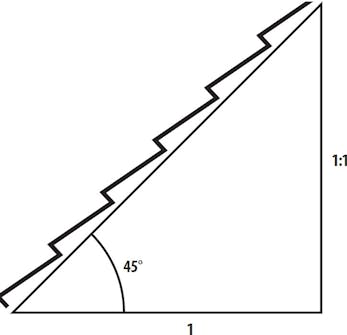
30 graderär en inte lika vanlig vinkel, men som du kan se nedan förekommer den som spets i en triangel när ena hörnet är vinkelrätt.
Din allra vanligaste fog är garanterat i rät vinkel, och det är den när två lister sätts ihop med kortsida mot långsida.
En gerad fog i 45 graders vinkel är också otroligt vanlig, och den förekommer framför allt i tavel- och spegelramar.
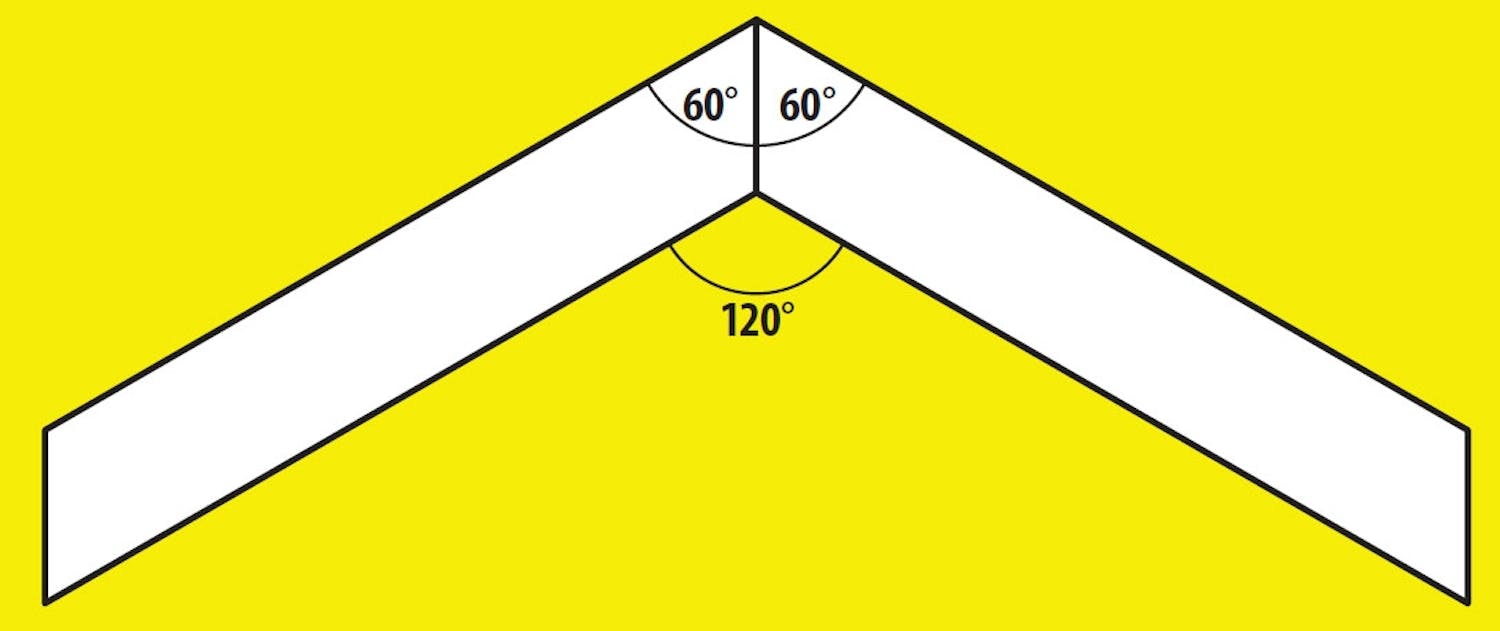
60 grader används bland annat till en sexkantig ram, där de yttre hörnen är 120 grader (dvs. 60 + 60 grader).
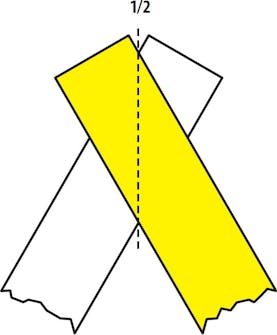
Halva vinklar ger snygga hörn
Stora avstånd kräver stora vinklar
Exakt arbete med okända mått
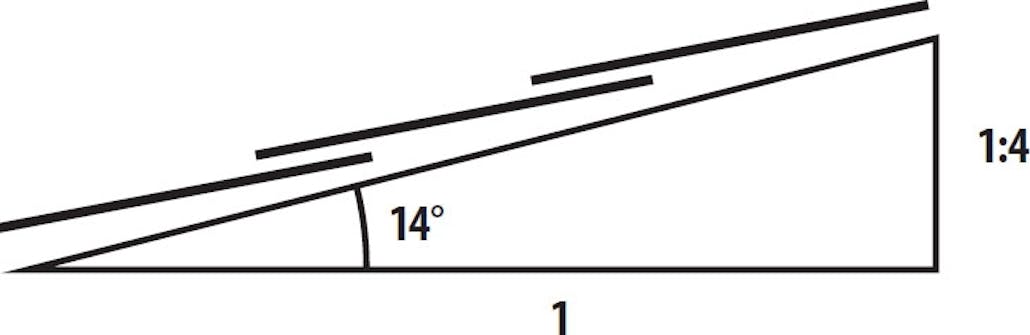
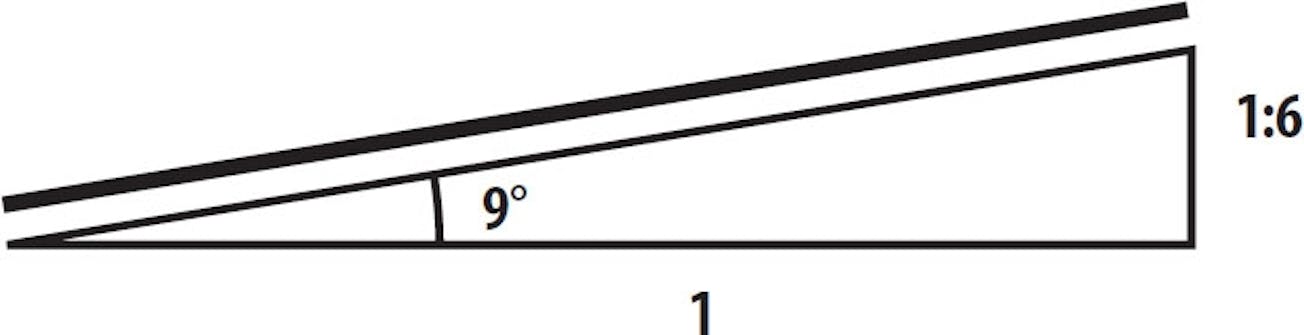
Använd ett förhållande när du skapar fall på terrassen
Bestäm taklutningen
Hängrännans fall mäts i millimeter
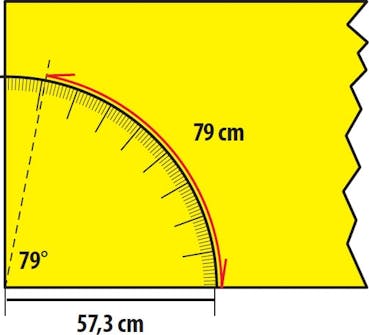
Perfekt vinkel när avståndet är stort
VIDEO: Vinkel till större projekt
Den gör du själv av tre brädor